CONS-TD
Proiectul își propune să dezvolte unele contribuții la teoria ecuațiilor diferențiale întârziate (DDE) și a sistemelor comutate prin dezvoltarea, în principal, a condițiilor necesare și suficiente pentru stabilitatea punctelor de echilibru și reducerea caracterului conservativ al condițiilor suficiente date de utilizarea mai multor funcționale Lyapunov-Krasovskii.
Rezultate – Etapa I
Etapa 1 „Studii preliminare privind conditiile de stabilitate pentru sisteme de ecuatii diferentiale cu intarziere si comutare liniare si neliniare si modalitati de reducere a conservativitatii acestor conditii” cuprinde urmatoarele activitati:
Act 1.1 – State-of-the-art privind conditiile de stabilitate ale sistemelor de ecuatii diferentiale cu intarziere si comutare;
Act 1.2 – Evaluarea gradului de conservativitate.
Un prim model reprezentativ considerat este al unui sistem cu intarziere, cazul liniar, cu perturbatie si cu intarziere pe controlul cu reactie dupa stare
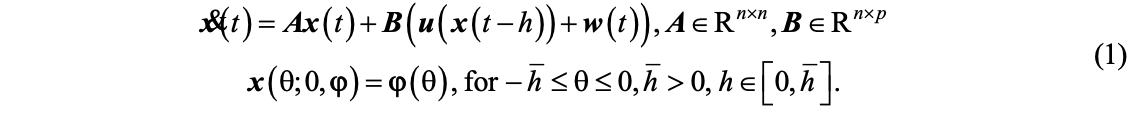
Un al doilea model este al unui sistem liniar perturbat, cu intarziere pe control si cu comutari controlabile, dependente de timp (ambele modele pot descrie lantul de comanda a zborului avionului)
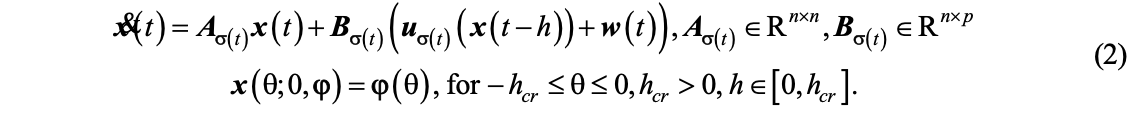
Semnalul de comutare σ, este o functie constanta pe portiuni
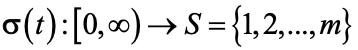
Conceptele cu care se opereaza sunt: stabilitate intrare-stare (ISS), stabilitate „minimum dwell time d*” unde

Instrumentul matematic utilizat frecvent in studiul stabilitatii este functionala Liapunov-Krasovskii (LKF). In decursul Etapei s-a obtinut o teorema de stabilitate (ISS) pentru sistemul (1) si s-a analizat o teorema de stabilitate ISS preluata din literatura. Mecanismul demonstratiilor este laborios si conduce la conditii de stabilitate mai mult sau mai putin conservative.
O prima concluzie este ca pe aceasta cale a LKF este putin probabil, daca nu imposibil, de a obtine conditii neconservative de stabilitate. O sugestie a dificultatii poate transpare din faptul ca problema poate fi pusa in forma unei probleme de optimizare multiobiectiv cu constrangeri: minimize
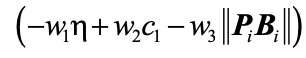
subject to:
a)

b)
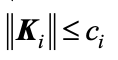
c)
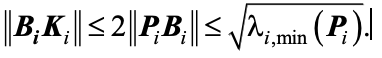
A doua concluzie este aceea a schimbarii de paradigma: o metoda care sa dezvolte sugestiile provenind din unele lucrari precum [G. Chesi, P. Colaneri, J. C. Geromel, R. Middleton and R. Shorten, „A Nonconservative LMI Condition for Stability of Switched Systems with Guaranteed Dwell Time]. Metoda foloseste functii Liapunov polinomiale omogene, idee avandu-si originea in celebra Problema nr 17 a lui Hilbert. O a doua cale ce urmeaza a fi dezvoltata porneste de la convexificarea unor conditii ca aceea data mai sus (a se vedea W. Xiang et al., Nonconservative lifted convex conditions for stability of discrete-time switched systems under minimum dwell-time constraint, IEEE Transactions on Automatic Control, Volume: 64, Issue: 8, August 2019).
Diseminrea rezultatelor:
1. Critical case of stability for a nonlinear switched system of delay differential equations with applications to a hydraulic servomechanism – D. Enciu, A. Halanay, I. Ursu, 11th International Conference on Pure and Applied Mathematics (ICPAM 2022), 12-22 July 2022, Bratislava, Slovakia
Abstract
In this paper the complex problem of nonlinear dynamical system with simultaneously critical case for stability, time-delay on state, and an autonomous uncontrolled state dependent switching rule is addressed. A general theorem ensuring simple stability for this type of system is given. This leads to the application of a Malkin-type mathematical apparatus, combined with the use of multiple complete Lyapunov-Krasovskii functionals. Since the characteristic equation of the linear approximation has a null eigenvalue, following some transformations of variables, the initial system consisting of five nonlinear differential equations is decomposed in the canonical form of Malkin approach which consists of a fourth order system and a first order system that contains only nonlinear terms. The equilibrium stability condition of the nonlinear system returns to the fulfillment of the asymptotic stability condition of the linearized equations and the Lyapunov conditions.The mathematical model is applied to the analysis and synthesis of electrohydraulic servomechanism. This real world object is vital for flight safety being an essential equipment in aircraft flight controls. Thus, some thresholds of admissible delay for ensuring the stability of the servomechanism are determined.
2. New strategy for the safety and comfort of the passengers and aircraft crew during atmospheric turbulence – D. Enciu, I. Ursu, G. Tecuceanu, 7th European Conference on Structural Control (EACS 2022), 10-13 July 2022, Warsaw, Poland
Abstract
An airplane trip can be psychological terrifying for any traveler. If, during the flight, the airplane meets a turbulent air front, then the scenario is perfect for a Hollywood movie, and the panic among passengers increases proportionally with the severity of the turbulence. In this paper, a new approach of the turbulence mitigation methodology is proposed based on a solid background using an active control vibration. The experimental model is represented by a realistic, elastic airplane wing model controlled by an electric linear servoactuator. The mathematical model is completed by numerical simulations and experiments in the subsonic wind tunnel upgraded with a turbulence generator. The qualification of an emergent technology of this type will have double impact: for the passengers – safety and mental comfort increasing given by the significant reduction of the dynamic effects produced by the turbulent field; for the airplane – weight optimization based on the loads control generated by the atmospheric turbulence.
3. A critical case for stability in a model of an electrohydraulic servomechanism – D. Enciu, A. Halanay, I. Ursu, 29th Conference on Applied and Industrial Mathematics (CAIM 2022), 25-29 August 2022, Chisinau, Republica Moldova
Abstract
In this paper, the conditions required for the stability of a nonlinear system with time-delay and switching are studied. The starting point of the theory is based on a real-world mathematical model of an electrohydraulic servomechanism located in ailerons flight controls of the Romanian IAR 99 Hawk jet training airplane. For this model, a general theorem on the equilibrium stability in a critical case for a switched nonlinear system of delay differential equations is stated. The framework uses multiple complete Lyapunov-Krasovskii functionals. The characteristic equation has one zero root which claims the use of a special approach given by a Lyapunov-Malkin theorem. Therefore, some transformations are made to write the linearized system in a canonical form where the stability Lyapunov theorem of the linear approximation can be applied. The study of the stability of equilibria relies on two conditions: a Lyapunov condition and an asymptotic stability condition. The transformation of the nonlinear system into the specific form of the Lyapunov-Malkin theorem and the verification of the two conditions mentioned above requires a double perspective – analytical developments and numerical simulations – since the mathematical models are too complex to be approached only analytically. Accordingly, an important result is calculated, regarding an admissible delay threshold in preserving stability of the electrohydraulic servomechanism as vital system for the safety of the aircraft. Some considerations regarding the conservatism and the non-necessity of sufficient conditions conclude the work.
4. Lyapunov-Malkin type approach of equilibrium stability in a critical case applied to a switched model of a servomechanism with state delay – D. Enciu, A. Halanay, A. Toader, I. Ursu, accepted for publication in International Journal of Control
Abstract
A general theorem on equilibrium stability in a critical case is applied to switched strong nonlinear differential equations with time delay on state, characterizing electrohydraulic servomechanisms dynamics. Basically, its proof involves the use of the Lyapunov-Malkin approach to stability and multiple complete Lyapunov-Krasovskii functionals. The fulfilment of the equilibrium stability condition of the nonlinear system returns to the asymptotic stability condition of the linearized equations and to the so-called Lyapunov conditions for the latter. The transformation of the nonlinear system into the canonical form specific to the Lyapunov-Malkin theorem, and the verification of the two conditions mentioned above require analytical developments doubled by numerical simulations, since the mathematical models are too complex to be approached only analytically. As a consequence, an important result is obtained, for the first time, regarding the thresholds of admissible delay in preserving the stability of a real world object, vital for the safety of the aircraft.
Rezultate – Etapa II
Etapa 2 „Dezvoltarea unor modele matematice pentru sisteme de ecuatii diferentiale cu intarziere si comutare pentru caracterizarea unor structuri aeroelastice. Elaborarea unor conditii necesare si suficiente de stabilitate in sens Lyapunov ale punctelor de echilibru pentru sisteme de ecuatii diferentiale cu intarziere si comutare – teoreme de stabilitate” cuprinde urmatoarele activitati:
Act. 2.1 – Dezvoltarea de modele matematice pentru actionarea suprafetelor de comanda primare ale avionului;
Act. 2.2 – Dezvoltarea de modele matematice pentru controlul activ al aripei in tunelul aerodinamic;
Act. 2.3 – Metoda functiilor Lyapunov polinomiale pentru elaborarea conditiei necesare si suficiente de stabilitate;
Act. 2.4 – Tur de orizont pentru alte abordari ale conditiilor necesare si suficiente de stabilitate.
Activitatile au fost realizate in cadrul Etapei 2 cu realizarea Obiectivului O1 aferent: obtinerea unor conditii necesare si suficiente de stabilitate in sens Lyapunov pentru sisteme de ecuatii diferentiale liniare si neliniare cu intarziere si switching. Astfel se pregateste cadrul pentru Etapa a 3-a de sinteza a unor legi de control activ si simulari numerice.
Stabilitatea este o condiție sine qua non a fiecărui sistem. Prin urmare, efortul de cercetare este îndreptat spre construirea unor sisteme stabile garantate. În marea majoritate a cazurilor, acestea sunt exprimate prin condiţii suficiente, conservative (restrictive), care uneori impun criterii drastice, greu de îndeplinit, şi practic inutile, deoarece sistemul poate să fie stabil chiar dacă aceste criterii nu sunt îndeplinite. Se incearca gasirea unei teorii unificatoare atât a sistemelor cu întârziere, cât și a celor cu comutare, astfel incat problema foarte importantă a reducerii conservativității condițiilor sufficient sa asigure stabilitatea punctelor de echilibru.
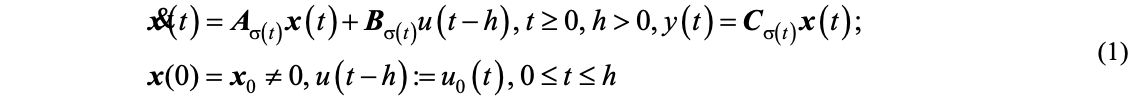
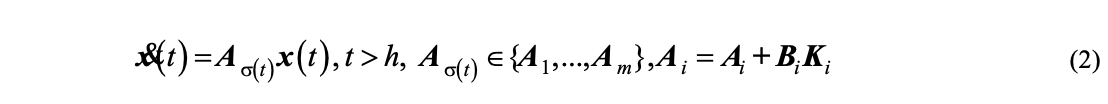
Contributia etapei se rezuma in esenta la 3 teoreme:
1) demonstrarea unei propozitii privind implementarea conditiei de eludare a intarzierii prin feedback predictiv de stare;
2) o prima teorema, dand o conditie conservativa de stabilitate, demonstrata in detaliu pentru a intelege mecanismele teoriei;
2) o a doua teorema, citata din literatura, dand o conditie neconservativa, dar practic inoperanta;
3) o a treia teorema, furnizand conditii neconservative de stabilitate, dar care presupune, ca in celebra problema a celor patru culori rezolvata de Appel si Haken in 1976, interventia calculatorului intr-un proces de convergenta matematica.
Diseminarea rezultatelor
1. Articol WoS
A. Toader, I. Ursu, Daniela Enciu, G. Tecuceanu, Towards nonconservative conditions for equilibrium stability. Applications to switching systems with control delay, Communications in Nonlinear Science and Numerical Simulation, 121 (2023) 107188
2. Proceedings BDI
I. Ursu, A. Toader, G. Tecuceanu, Daniela Enciu, Input-to-state stability of a time-invariant system with control delay and additive disturbances, Proceedings in Applied Mathematics and Mechanics 2023;e202300152.
3. Control synthesis and stability analysis of equilibria in a mathematical model of a pneumatic servosystem – D. Enciu, A. Halanay, C.-A. Safta, A. Toader, I. Ursu, ICNPAA: Mathematical Problems in Engineering, Aerospace and Science (ICNPAA 2023), 27-30 June 2023, online
Abstract. A study on the stability of equilibrium points of a nonlinear system, representing the mathematical model of a pneumatic servomechanism, is developed. The characteristic equation of the linearized system appears to have a zero eigenvalue, therefore placing the problem in a critical case of stability. The solution requires the approach of Lyapunov-Malkin paradigm.
4. Input-to-state stability of a time-invariant system with control delay and additive disturbances – I. Ursu, A. Toader, G. Tecuceanu, D. Enciu, 93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2023), 30 May – 2 June 2023, Dresden, Germany
Abstract. We consider a class of linear time invariant systems with control delay and additive disturbances. A state predictive feedback method is first applied to compensate the actuator delay. In this way, a closed loop system free of delay is achieved. It allows to ensure input-to-state-stability of the closed loop system. Applications are given for the lateral-directional stability of an airplane with two controls, on the aileron and on the rudder, in correlation with compliance with some regulatory flight conditions.
5. On a critical case for the stability of equilibria of a nonlinear switched system with state delay – D. Enciu, A. Halanay, I. Ursu, 5th International Applied Mathematics, Modelling and Simulation Conference (AMMS 2023), 14 -17 July 2023, Leipzig, Germany
Abstract. In this article, a stability problem in critical case is considered for a real world system, a hydraulic servomechanism, characterized by a nonlinear dynamic mathematical model, with state delay and structural switching. Solving the problem involves the use of the mathematical tool of Lyapunov Malkin critical stability, completed with the apparatus of multiple Lyapunov Krasovskii functionals. To apply this solution strategy, the mathematical model of the system is brought to the canonical form specific to the Lyapunov Malkin stability analysis. The stability condition of the nonlinear system returns to the fulfillment of the asymptotic stability condition of the linearized system, to which is added the fulfillment of a condition called the Lyapunov condition. The analysis of the fulfillment of these conditions is done analytically numeric. Finally, the conclusive result of the work consists in determining the critical delay of the system.
6. Further results on the input to state stability of a linear system with control delay – D. Enciu, I. Ursu, 12th International Conference on Pure and Applied Mathematics (ICPAM 2023), 17 – 21 July 2023, Porto, Portugal
Abstract. This paper presents a class of linear perturbed systems with control delay and for which stabilizing feedback is available. Through a Lyapunov-Krasovskii approach, by using the Jensen inequality, the Leibniz integral rule and a double Hadamard inequality, sufficient input-to-state stability conditions in terms of size of the delay is obtained.
7. On the stability of a time-invariant linear system with time-delay and disturbances with application to aerospace engineering – D. Enciu, I. Ursu, A. Toader, 30th Annual Conference on Applied and Industrial Mathematics (CAIM 2023), 14 – 18 September 2023, Iasi, Romania
Abstract. The beauty of the mathematical equations is highlighted by presenting a practical, real application in controlling the flight stability of an airplane in a turbulent atmospheric field. This paper presents a linear mathematical model with actuator delay in the control chain and external disturbances. The time-delay is compensated by applying a state predictive feedback method and the perturbation is treated according to the basic Kolmogorov concept.
8. The stability of a linear time-invariant system with control delay. Application to the stability of the aircraft control chain in conditions of atmospheric turbulence – A. Toader, D. Enciu, I. Ursu, 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023), 12-16 November 2023, Rome, Italy
Abstract. A class of time-invariant linear systems with control delay and additive disturbances is considered. Through a predictive state feedback method, the control delay is compensated, reaching a closed-loop system without delay. Based on a theorem of F. Mazenc, S.-I. Niculescu, M. Krstic, stability is ensured in the presence of disturbances. The application is made on the control chain of an airplane, in the presence of Dryden-type atmospheric turbulence.
Rezultate – Etapa III
Etapa 3 se numeste „Sinteza unor legi de control activ. Simulari numerice” si cuprinde urmatoarele activitati:
Act. 3.1 – Aplicatii de control activ stabil asupra modelului matematic al aripei in tunelul aerodinamic prin simulare numerica
Act. 3.2 – Analiza conditiilor de stabilitate
Activitatile au fost realizate in cadrul Etapei 3 cu realizarea Obiectivului general de dezvoltare a unui cadru matematic pentru obtinerea unor conditii necesare si suficiente pentru stabilitatea punctelor de echilibru ale unor ecuatii diferentiale cu intarziere si comutare cu reducerea conservativitatii conditiilor suficiente date de utilizarea functionalelor multiple Lyapunov-Krasovskii si aplicarea acestora in cazul modelarii unor obiecte apartinand lumii reale – aripa de avion cu eleron.
Contributiile principale se rezuma in esenta la:
- dezvoltarea unei abordări unitare a stabilității non-conservative a unui sistem liniar cu comutare, cu intarziere pe control, sistem care apartine lumii reale;
- utilizarea unui control feedback predictive de stare pentru a converti sistemul cu comutare cu întârziere pe control într-un sistem cu comutare fără întârziere;
- atestarea implementabilității controlului feedback predictive de stare
- demonstrarea unei teoreme care oferă o condiție conservatoare a stabilității exponențiale uniforme globale, ca punct de plecare în abordarea neconservativității
- soluție pentru cele două variante echivalente prin discretizare și dovada că versiunile de operare online și analiză offline dau, așa cum era de așteptat, același rezultat;
- soluție pentru condițiile LMI neconservative prin utilizarea unor algoritmi de programare SOS cu adăugarea unui algoritm de calcul al dwell time dat de o diagrama logică
- aplicarea, pentru prima dată după cunoștințele noastre, a teoriei nonconservativității bazată pe algoritmi de programare SOS la un obiect din lumea reală: un model fizic al unei aripi inteligente de avion într-un tunel subsonic
- realizarea unui rezultat substanţial al simulărilor: obtinerea dwell timp minim garantat care caracterizează stabilitatea de echilibru a sistemului de comutare cu întârziere de control.
- sinteza si aplicarea unei legi de control pentru stabilitatea lateral-directionala a unei aeronave in prezenta unei perturbatii.
Diseminarea rezultatelor
Articol WoS
Enciu, D.; Toader, A.; Ursu, I. Further Results on the Input-to-State Stability of a Linear Disturbed System with Control Delay. Mathematics 2024, 12, 634. https://doi.org/10.3390/math12050634; IF: 2.4

